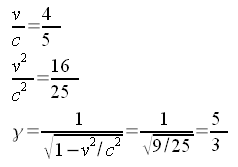
Zu meiner Berechnung des Zwillingsparadoxons wurde ich schon oft gefragt, wie es sich denn verhalten würde, wenn zwei Reisende gleichartige Bewegungen in unterschiedliche Richtungen durchführen. Diesen Fall möchte ich hier als Drillingsparadoxon vorstellen.
Man stelle sich Drillinge vor, von denen einer auf dem Heimatplaneten zurückbleibt, während die anderen beiden schnelle Raumschiffe besteigen, in entgegengesetzte Richtungen losfliegen, nach einer gewissen zurückgelegten Strecke ihr Raumschiff wenden und mit gleicher Geschwindigkeit zurückkehren. Der auf der Erde verbliebene Drilling wird dann älter sein, als seine beiden Brüder. Diese werden aufgrund ihrer identischen Flugabläufe um den gleichen Betrag weniger gealtert sein.
In der einfachsten Variante, die hier betrachtet werden soll, sind die Beschleunigungsphasen der beiden Reisenden vernachlässigbar kurz und ihre Geschwindigkeiten auf Hin- und Rückreise konstant. Die Geschwindigkeit v werde ich auf den Bildern zu 80% der Lichtgeschwindigtkeit annehmen. Das ist der Wert, den ich auch beim Zahlenbeispiel zum Zwillingsparadoxon angenommen habe und bei dem sich einfache Brüche für die wichtigen Faktoren ergeben:
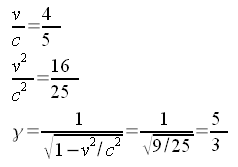
Unabhängig von diesen Werten sind jedoch alle Formeln allgemeingültig gehalten.
Um eine übersichtlichere Darstellung zu erreichen werde ich die Zeit t wie üblich nach oben und die Entfernung x nach links und rechts auftragen. Solch ein Diagramm, das Raum-Zeit-Diagramm, habe ich im nächsten Bild dargestellt:
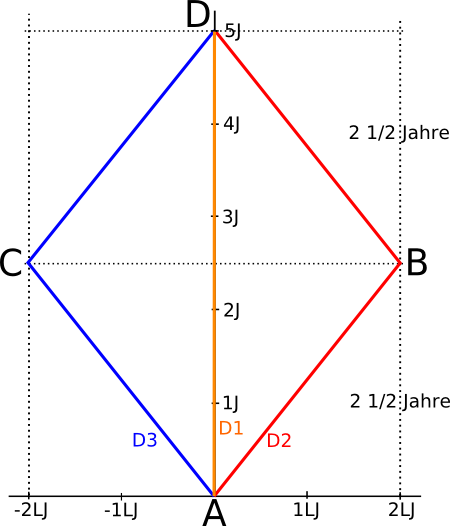
Die orange Linie stellt den Ort des daheim bleibenden Drillings in Abhängigkeit von der Zeit dar. Es ist eine senkrechte Linie, die einfach bedeutet, dass sich dieser Drilling nicht bewegt. Ich habe ihn ganz profan D1 genannt.
D1 verabschiedet sich von seinen Brüdern am Raum-Zeit-Punkt A mit den Koordinaten tA=0 und xA=0. Er trifft die beiden am selben Ort xD=0 aber nach fünf Jahren (tD=5 Jahre) wieder. Diese Fünf Jahre ergeben sich einfach aus der Entfernung von vier Lichtjahren hin und zurück, die die beiden Reisenden mit einer Geschwindigkeit von 4/5 Lichtgeschwindigkeit zurücklegen.
Drilling D2 fliegt 2 1/2 Jahre in positive x-Richtung und erreicht im Moment B, in zwei Lichtjahren Entfernung seinen Wendepunkt. Dann fliegt er zurück um D1 am Punkt D zu treffen. Drilling D3 fliegt gleichzeitig mit D2 in die Gegenrichtung los und führt exakt die selben Manöver spiegelverkehrt aus. Alle Drillinge treffen sich also Gleichzeitig an den Koordinaten D.
Die Koordinaten aller wichtigen Raum-Zeit-Punkte habe ich in folgenden Formeln angegeben
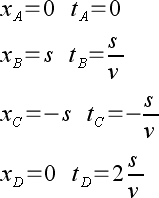
wobei s die einfache Entfernung der Wendepunkte B und C vom Heimatplanten und v die Geschwindigkeit der beiden reisenden Drillinge ist.
Nach der speziellen Relativitätstheorie vergeht die Zeit für ein in einem Inertialsystem bewegten System langsamer als für ein ruhendes System. Diese Regel gilt gleichartig in jedem beliebigen Inertialsystem. Die Eigenzeit τ einer bewegten Uhr berechnet sich zu:

Bei dem Gammafaktor von 5/3 ergibt sich also, dass für die beiden Reisenden zu jeweils drei Jahre vergehen, während der zuhause gebliebene fünf Jahre misst. Das ist die Zeitdilatation.
Dass für beide Reisende die gleiche Zeit vergeht, kann man bereits aus der Symmetrie des Vorgangs erkennen. Beide Reisenden bewegen sich jederzeit mit der selben Geschwindigkeit durch das Koordinatensystem, in dem der Drilling D1 ruht. Diese Symmetrie besteht jedoch nicht, wenn man die Reisen in einem anderen Inertialsystem betrachtet:
Ich möchte nun mit einer Lorentztransformation zeigen, wie sich die Situation in einem Inertialsystem darstellt, in dem Drilling D3 zunächst ruht. Die Transformation in ein solches Koordinatensystem ist mathematisch recht einfach und wird durch diese Formel beschrieben:
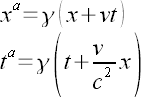
Das ist die Lorentztransformation. Mit ihr werden die Koordinaten x und t in die Koordinaten xa und ta umgerechnet. In der Literatur findet man die Lorentztransformation meist mit negativem Vorzeichen (x-vt). Hier sind die vorzeichen positiv, da sich das Koordinatensystem xa, ta gegenüber x, t nach links, also zu negativen Werten bewegt.
Setzt man nun die Koordinaten der vier relevanten Ereignisse A, B, C und D in die Lorentztransformation ein, so erhält man diese Ereignisse in den neuen, nicht symmetrischen Koordinaten:

Die Lorentztransformation ist eine lineare Koordinatentransformation. Das bedeutet, dass alle geraden Linien auch nach der Transformation gerade bleiben. Man kann also die neuen Wege der Drillinge in ein Diagramm einzeichnen, indem man die vier neu berechneten Ereignisse an den richtigen Zeiten und Orten einzeichnet und sie durch gerade Wege verbindet. Das habe ich im folgenden Bild getan:
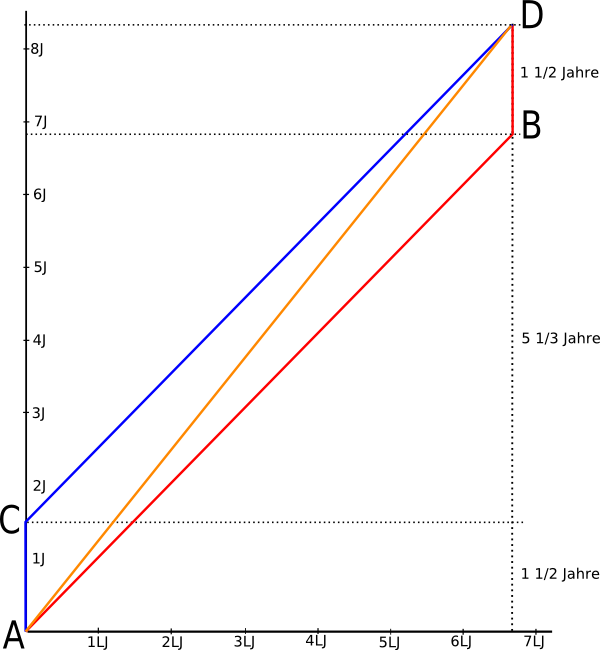
In diesem Inertialsystem bewegt sich die Erde die ganze Zeit mit konstanter Reisegeschwindigkeit. Die Dauer des gesamten Ablaufs ist nun um den Gamma-Faktor verlängert und beträgt 8 1/3 Jahre, statt der fünf Jahre im Koordinatensystem mit ruhender Erde. Die Bewegung der beiden Reisenden ist in diesem Koordinatensystem nicht gleich. D2 reist die ganze Strecke von 6 2/3 Lichtjahren in nur 6 5/6 Jahren und wartet dort die letzten 1 1/2 Jahre auf das Eintreffen der Erde. D3 ruht dagegen die ersten 1 1/2 Jahre und legt die 6 2/3 Lichtjahre dann zurück um D2 und D1 am Punkt D zu treffen. Beiden Reisenden ist aber gemein, dass sie von der gesamten Dauer des Vorgangs 1 1/2 Jahre im Koordinatensystem ruhen und sich 6 5/6 Jahre lang mit 40/41 der Lichtgeschwindigkeit bewegen. Es ist also klar, dass für beide Reisenden insgesamt die gleiche Zeit vergeht. Aber dass dieses Diagramm genau die selben Messwerte für alle Beteiligten ergibt, wie das Diagramm mit der ruhenden Erde oben im Bild, lässt sich erst nach einer weiteren Rechnung erkennen.
Oben haben wir gerechnet, dass der auf der Erde verbleibende Drilling D1 fünf Jahre misst, während für D2 und D3 je nur drei Jahre vergangen sind. Damit beide Koordinatensysteme konsistent die selbe Situation beschreiben, müssen auch in dem Inertialsystem, in dem zunächst D3 ruht, die selben Zahlen herauskommen.
Die Erde bewegt sich in diesem Bild 8 1/3, also 25/3 Jahre lang mit 4/5 der Lichtgeschwindigkeit. Dies entspricht einem Gamma-Faktor von 5/3 (wie oben angegeben). Die einfache Rechnung ergibt, dass auf der Erde (25/3)/(5/3)=5 Jahre gemessen werden. Das entspricht genau der Zeit im ersten Bild.
Die Drillinge D2 und D3 verbringen in diesem Bild jeweils 1 1/2 Jahre ruhend. Hier ist nichts zu rechnen. Sie messen auch genau diese Zeit. Die restlichen 6 5/6 =41/6 Jahre bewegen sie sich mit einer Geschwindigkeit von 40/41 der Lichtgeschwindigkeit. Das ergibt einen Gamma-Faktor von 41/9. Sie messen also in diesem Abschnitt eine vergangene Zeit von (41/6)/(41/9)=3/2= 1 1/2 Jahren. Insgesamt vergehen also für die beiden Reisenden auch dann 3 Jahre, wenn man die Situation in diesem Koordinatensystem ausrechnet.
Dieses Drillingsparadoxon ist ein einfaches Rechenbeispiel zur speziellen Relativitätstheorie. Es zeigt, wie Lorentztransformationen anzuwenden sind und wie dann die Zeitdilatation ganz von selbst richtig herauskommt. Es zeigt auch einmal mehr, dass die spezielle Relativitätstheorie keine Widersprüche enthält. Das Zwillingsparadoxon kann auch für mehrere Reisende durch richtiges Nachrechnen aufgelöst werden. Es ist nichts paradoxes an der speziellen Relativitätstheorie. Sie ist nur etwas gewöhnungsbedürftig.
Letzte Änderung: 25.12.2008
© Joachim Schulz