Die Lorentz-Transformation ist eine Transformation innerhalb einer vierdimensionalen Raumzeit. Für uns Menschen sind vier Dimensionen schwer vorstellbar. Zum Glück lassen sich aber viele Probleme mit nur einer räumlichen Dimension und einer zusätzlichen für die Zeit erklären. Das kann man dann auch grafisch darstellen, indem man die räumliche Achse (als x-Achse bezeichnet) in horizontaler Richtung zeichnet und die Zeitachse (hier als t-Achse manchmal als ct-Achse bezeichnet, hier aber c=1, also ct=t) in vertikaler Richtung.
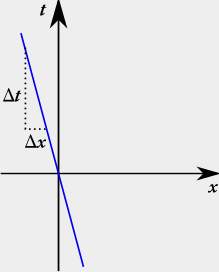
Wenn sich ein Körper mit konstanter Geschwindigkeit entlang der x-Achse bewegt, dann ändert sich nach der Zeit t kontinuierlich seine Position x(t) = vt entlang der x-Achse. Bei konstantem v ist diese Gleichung eine Geradengleichung, allerdings mit den Variablen x und t und nicht mit x und y, wie man das normalerweise gewohnt ist. Ein solches Diagramm würde also etwa so aussehen:
Dabei ist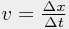 
die Geschwindigkeit des beschriebenen Objektes. Das selbe kann man auch mit einem Objekt machen, das sich nach links (also in negative x-Richtung) bewegt:
In einem solchen Diagramm kann man aber auch die t'- und x'-Achsen eines bewegten Systems darstellen. Wir wollen nur den Spezialfall betrachten, bei dem die Relativgeschwindigkeit in negative x-Richtung geht (also nach links) und zum Zeitpunkt t=t'=0 die Ursprünge beider Koordinaten am selben Ort sind, also x=x'=0 ist:
Hierbei fällt auf, dass die Achsen nicht einfach in eine Richtung gedreht werden, sondern sich die x'-Achse nach rechts dreht, wenn die t'-Achse nach links kippt und umgekehrt. Das ergibt sich direkt aus der Lorentztransformation. Dabei ist besonders wichtig, dass die x- und x'-Achse nicht zusammen fallen. Diese Eigenschaft der Lorentztransformation bezeichnet man als Relativität der Gleichzeitigkeit. Ereignisse, die in einem System gleichzeitig statt finden (z. B. zum Zeitpunkt t=0, also auf der x-Achse), tun dies nicht mehr unbedingt in einem anderen relativ dazu bewegten System, außer wenn die Ereignisse auch noch am selben Ort statt finden.
In einem solchen Diagramm kann man auch das Feld einer stehenden Welle darstellen. So kann man sehen, welche Stärke das elektrische Feld an einem bestimmten Ort und zu einer bestimmten Zeit hat. Für den Fall des stehenden Lasers sieht das ganze dann so aus:
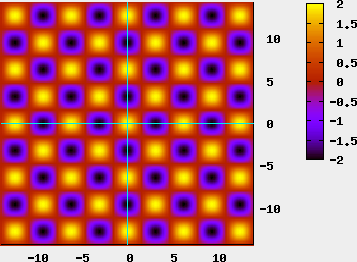
In diesem Diagramm ist die Feldstärke zu bestimmten Zeitpunkten und Orten durch einen Farbencode dargestellt. Man kann das Diagramm mit dem animierten Plot vergleichen. Wenn man sich das Feld entlang der x-Achse bei fester Zeit t=0 betrachtet, hat man eine Standbild-Aufnahme der Situation bei einer festen Zeit t=0. Wenn man einen Schnitt bei einer Parallelen zu der x-Achse macht, dann sieht man die Situation zu einem entsprechend anderen Zeitpunkt. Man kommt gedanklich also durch parallele Schnitte durch das Minkowski-Diagramm auf die Animation, indem man sich die Situation zu immer späteren Zeitpunkten betrachtet.
Das selbe kann man auch mit dem bewegten Laser machen. Das sieht dann in etwa so aus (beta=0,3; gamma=1,05):
Ich habe hier noch zusätzlich die Achsen des Laser-Ruhesystems in schwarz mit eingezeichnet. Das Bild wurde mit den selben Formeln der Interferenz von zwei dopplerverschobenen Wellen erzeugt, wie die Animationen auch. Allerdings könnte man auch jeden einzelnen Farbpunkt in dem Diagramm des stehenden Lasers einfach mit der Lorentztransformation umrechnen und würde auf das selbe Ergebnis kommen.
Um erkennen zu können, wie sich die etwas kompliziert anmutende Welle in der Animation ergibt, schauen wir uns das ganze einfach etwas gekippt an:
Wenn man sich die Vorderkante dieser Darstellung anschaut, kann man wieder die bekannte Wellenform erkennen. Bei dieser Kante ist die Zeit bei einem festen Wert konstant, es ist also ein Standbild. In der Animation entspricht jedes Einzelbild einem solchen Schnitt durch dieses "Gebirge". Der Kurvenverlauf der Feldstärke des elektrischen Feldes ergibt sich also vor allem daraus, dass nicht nur die t'-Achse gekippt ist, sondern auch die x'-Achse und damit ist er letztendlich eine Folge der Relativität der Gleichzeitigkeit.
Letzte Änderung: 05.11.2005
© Gastbeitrag von Marco Rothley