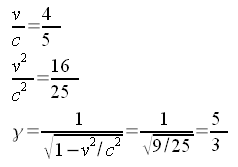
Nachdem ich das Zwillingsparadoxon durchgerechnet habe, gebe ich auf dieser Seite ein einfaches Zahlenbeispiel. Sehr einfach werden die Formeln, wenn man annimmt, dass der Reisende mit 80% der Lichtgeschwindigkeit unterwegs ist. Dann gilt:
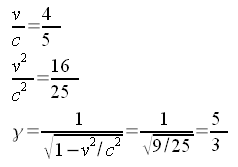
Nimmt man weiterhin an, dass der zu besuchende Planet nur zwei Lichtjahre entfernt ist, so kommt man auf folgendes Bild:
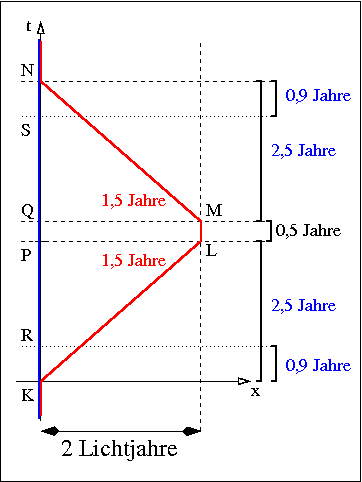
Aus der Sicht der ruhenden Erde braucht man mit 80% Lichtgeschwindigkeit 2,5 Jahre um 2 Lichtjahre zurückzulegen. Bei einem Gammafaktor von 5/3 bewirkt die Zeitdilatation, dass auf dem Raumschiff nur 1,5 Jahre vergehen. Die Besatzung altert also pro Reise um ein Jahr weniger als die Erdbewohner. Für Hin- und Rückreise macht das zwei Jahre. Die Ereignisse R und S auf der Erde geschehen 0,9 Jahre nach dem Start beziehungsweise vor der Landung auf der Erde.
Aus der Sicht des Reisenden ergibt sich folgendes Bild:
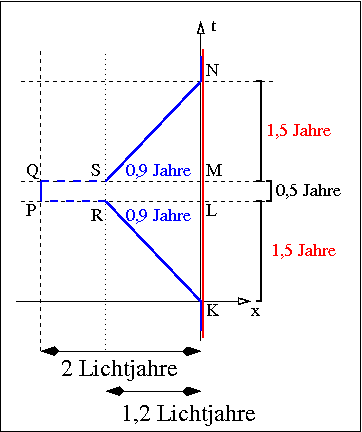
Während der Hin- und Rückreise erscheint die Entfernung von der Erde zum Planeten aufgrund der Längenkontraktion auf 1,2 Lichtjahre verkürzt. Die Reise dauert, wie oben geschrieben, 1,5 Jahre. Auf der (von der Rakete aus betrachtet) schnell bewegten Erde vergehen während des Fluges aufgrund der Zeitdilatation nur 0,9 Jahre. Die Rakete erreicht den Planet gleichzeitig mit dem Ereignis R auf der Erde.
Während des Abbremsens verzerrt sich jedoch die Weltsicht der Besatzung so, dass die Entfernung wieder 2 Lichtjahre beträgt und Ereignis P mit der Ankunft gleichzeitig ist. Durch die beiden Verzerrungen bei Landung und Start auf dem Planeten ergibt sich auch aus der Sicht des Reisenden, dass auf der Erde insgesamt 5,5 Jahre vergehen, während der Reisende nur 3,5 Jahre erlebt. Das Zwillingsparadoxon ist also lösbar: Der Reisende altert weniger.
Letzte Änderung: 18.12.2005
© Joachim Schulz