
Auf dieser Seite möchte ich das wahrscheinlich bekannteste Gedankenexperiment zur Relativitätstheorie vorrechnen, das Zwillingsparadoxon. Dieses Gedankenexperiment beschreibt ein Zwillingspaar von denen ein Zwilling eine Reise zu einem Entfernten Planeten antritt, während der andere Zwilling auf der Erde zurückbleibt. Nach der Rückkehr stellen die Zwillinge fest, dass der Reisende nun jünger ist als der nicht gereiste Zwilling. Das folgende Bild veranschaulicht die Situation:

Die Variable s bezeichnet die Entfernung des fremden Planeten von der Erde. Die Reise des Zwillings beginnt zum Zeitpunkt 0 und gliedert sich in folgende Abschnitte:
Um eine übersichtlichere Darstellung zu erreichen kann man die Zeit t nach oben und die Entfernung x nach rechts auftragen. Solch ein Diagramm, das Raum-Zeit-Diagramm, habe ich im nächsten Bild dargestellt:

Diagramme dieser Art werden nach Hermann Minkowski Minkowski Diagramme genannt. Sie sind ein gutes Hilfsmittel um sich relativistische Effekte klar zu machen. Auch wenn ich der Einfachheit wegen oft von der Sicht der Erde oder der Sicht des Reisenden schreibe, sollte man immer im Auge behalten, dass es sich hier um Koordinatensysteme, also um eine mathematische Veranschaulichung der zeitlichen Abläufe und räumlichen Konstellationen handelt. Es wird nicht wirklich beschrieben was der Reisende sieht. Dazu müsste man zusätzlich die Laufzeiten des Lichtes in Betracht ziehen. Ein Ereignis, das jetzt nach meinem Koordinatensystem in zwei Lichtjahren Entfernung geschieht, bekomme ich natürlich erst in zwei Jahren zu sehen.
Im Diagramm sind folgende Ereignisse eingetragen:
Zusätzlich sind zwei weitere Ereignisse auf der Erde (R und S) eingezeichnet. Die Orte und Zeiten aller Ereignisse aus der Sicht der Erde sind in folgenden Formeln angegeben:

Die Variablen t und x bezeichnen immer die Ereignisse in einem Koordinatensystem, in dem die Erde ruht, Zeiten und Orte in dem Koordinatensystem, in dem der Reisende ruht, werden je nach seinem Bewegungszustand mit hochgestelltem Buchstaben a, b, c oder d dargestellt.
Das Bild oben zeigt die Vorgänge aus der Sicht mit ruhender Erde dargestellt. Nun möchte ich mit Hilfe der Lorentztransformation die Vorgänge aus der Sicht mit ruhendem Reisenden darstellen. Die Lorentztransformation ist in der Form
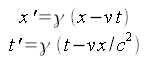
bekannt. Hierbei wird die Transformation aus der Sicht des Orts- und Zeitnullpunktes durchgeführt. Ich werde jedoch im folgenden die Transformation zu verschiedenen Zeiten durchführen. Die Lorentztransformation unter Beibehaltung der Zeit t0 am Ortsnullpunkt x=0 erfolgt nach folgender Formel:
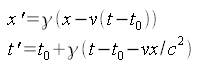
Diese Formel trägt dem Umstand rechnung, dass die Uhr des Reisenden nicht bei jeder Geschwindigkeitsänderung auf Null zurückgestellt werden soll. Die Transformation findet zum gegebenen Zeitpunkt t0 statt.
Der in der Formel verwendete Gamma-Faktor lautet:

Um die Vorgänge in den Koordinaten mit ruhendem Reisenden darzustellen ist für jede Beschleunigung (Änderung der Geschwindigkeit) eine Transformation notwendig. Dabei verwende ich unterschiedliche Geschwindigeiten v1 und v2 für Hin- und Rückreise, sowie die dazugehörigen Gamma-Faktoren. Zunächst für die Hinreise:
Die Hinreise beginnt zum Zeitpunkt Null, an dem beide Zwillinge am gleichen Ort x=0 sind. Um also in das Bezugssystem des Reisenden während der Hinreise zu Transformiern wird die gewöhnliche Lorentztransformation am Nullpunkt angewand. Die Koordinaten aus der Sicht der Hinreise werden dabei durch ein hochgestelltes a dargestellt:

Da die Beschleunigungen als so schnell angenommen werden, dass sie keine Zeit beanspruchen, ändert die Transformation weder die Zeit t_K noch den Ort x_K an dem die Beschleunigung stattfindet:

Für den Reisenden ist es interessant, wann er (nach seiner Uhr) am fremden Planeten ankommen wird. Dies stellt man durch Transformation der Landung L fest:

Der Reisende landet also schon nach einer um 1/gamma kürzeren Zeit. Das ist die Zeitdilatation der Relativitätstheorie. Der Ort 0 bedeutet, dass sich der Reisende nun am Ort der Landung befindet. Transformiert man nun auch das Ereignis P, an dem die Landung auf der Erde gefeiert wird, so erhält man:

Aus der Sicht der Hinreise findet diese Party also erst in der Zukunft statt. Der Reisende erlebt tatsächlich das frühere Ereignis R als Gleichzeitig mit seiner Ankunft am Planeten:
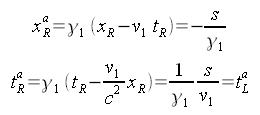
Das Ergebnis xRa=-s/γ bedeutet, dass die Erde im Moment der Ankunft (vor dem Abbremsen) näher erscheint als aus dem mit der Erde ruhenden Koordinatensystem. Dies ist die Längenkontraktion, sie entspricht genau der Zeitdilatation, so dass die relative Geschwindigkeit zwischen Erde und Reisenden aus beiden Perspektiven gleich erscheint.
Das Ereignis L bezeichnet die Landung auf dem Planeten. Zu diesem Zeitpunkt bremst der Reisende ab und beginnt seinen Forschungsaufenthalt:
Um die Weltsicht des Reisenden bei seinem Forschungsaufenthalt zu erhalten, wird die Lorentztransformation zur Zeit tLa durchgeführt:

Das Ergebnis ist relativ einfach. Der Reisende befindet sich im Verhältnis zur Erde in Ruhe, so dass es für ihn keine Längenkontraktionen gibt. Er sieht alles aus der Perspektive des Planeten am Ort s, so dass er alle Positionen um die Strecke s verschoben, also am Ort x-s wahrnimmt. Ausserdem zeigt seine Uhr eine etwas geringere Zeit, da seine Reise nur 1/gamma so lange gedauert hat, wie auf der Erde gemessen wurde.
Der Reisende führt nun für die Zeit τ (tau) seine Forschung durch. Und reist am Ereignis M ab in Richtung Erde. Das Ereignis M hat in seiner Messung die Koordinaten:

Zu diesen Koordinaten muss die Transformation in die Rückreise durchgeführt werden:

Hier habe ich angenommen, dass die Geschwindigkeit auf der Rückreise nicht unbedingt identisch zur Hinreise-Geschwindigkeit ist.
Das Ereignis Q, das zum Start der Rückreise gleichzeitig auf der Erde stattfindet, liegt nach der Transformation in der Vergangenheit:

Statt dessen ist nun das spätere Ereignis S gleichzeitig mit dem Rückreisestart:

Auch hier erkennt man wieder die Längenkontraktion. Die Entfernung zur Erde erscheint nach der Beschleunigung verkürzt.
Das Ende der Reise liegt wieder auf der Erde und wird als Ereignis N bezeichnet:

Zu diesem Zeitpunkt wird die letzte Beschleunigung und Transformation durchgeführt:
Die Transformation zurück in das Ruhesystem der Erde liefert folgendes Ergebnis:
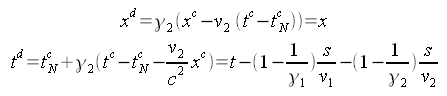
Um die Formeln nachzurechnen, braucht es eine etwas längere Nebenrechnung.
Wie zu erwarten sehen die Zwillinge jetzt wieder alles gleich (xd=x). Nur hat der gereiste Zwillings auf jeder der beiden Reisen eine kürzere Zeit erlebt.
Mit den jetzt errechneten Werten kann man ein Diagramm der Ereignisse aus der Sicht des Reisenden erstellen:
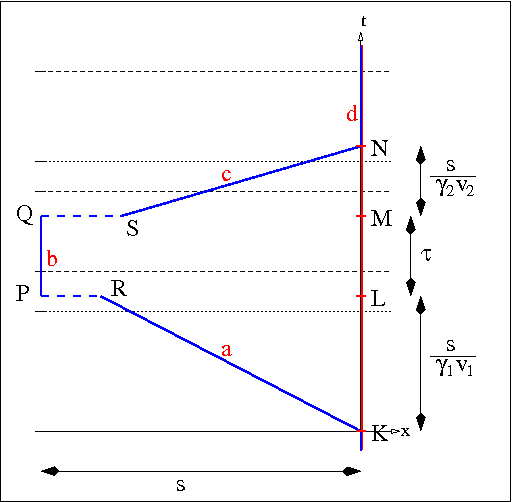
Der Reisende befindet sich stets an der Postition x'=0 in seinem Koordinatensystem. Er spürt aber zu den Ereignissen K, L, M und N jeweils eine Beschleunigung und damit einhergehend eine Verzerrung seiner Wahrnehmung von Raum und Zeit um ihn herum. Zum Start K bemerkt er die Längenkontraktion, aufgrund der ihm der Planet näher vorkommt und er kürzere Zeit bis zum Ereignis L, seiner Landung, braucht.
Während des Fluges sieht er die Erde sich entfernen und die Ereignisse auf der Erde langsamer vergehen. Als er am Planeten ankommt, findet auf der Erde gerade Ereignis R statt. Dieses Ereignis kann er noch nicht sehen, weil das Licht von dort noch lange braucht bis es ihn erreicht hat, aber er nimmt die Zeitdilatation der zu ihm bewegten Erde wahr und kann daraus berechnen, dass Ereignis R gleichzeitig mit seiner Ankunft (Ereignis L) stattfindet.
Die Abbremsung auf dem Paneten verändert wieder die Sichtweise des Reisenden und er sieht die Erde nun in gewohnter Entfernung zum Planeten und kann in seiner jetzigen Sichtweise berechnen, dass auf der Erde nun seine Ankunft auf dem Planeten gefeiert wird (Ereignis P). Auf der Erde ist nun mehr Zeit vergangen als für ihn. Bis zum Abflug erlebt er die gleiche Zeit, die auch auf der Erde vergeht.
Zum Start M passiert ähnliches wie bei der Landung: Vor der Beschleunigung ist das Ereignis Q gleichzeitig und die Erde befindet sich in gewohnter Entfernung. Nach der Beschleunigung ist der Abstand Erde-Planet längenkontrahiert und auf der Erde findet bereits das Ereignis S statt. Von diesem Ereignis bis zur Landung auf der Erde vergeht die Zeit auf der Erde langsamer, da sie sich relativ zum Reisenden bewegt.
Man sieht also, dass sich die scheinbaren Widersprüche des Zwillingsparadoxons im Rahmen der speziellen Relativitätstheorie lösen lassen, wenn man nur die Lorentztransformation richtig durchführt. Dass aus der Sicht des Reisenden die Erdzeit langsamer vergeht während für die Erdbevölkerung die Zeit des Reisenden langsamer vergeht, ist kein Widerspruch, wenn man die Verzerrung der Weltsicht während der Beschleunigungen berücksichtigt. Das ist die Relativität der Gleichzeitigkeit.
Der reisende Zwilling ist der, der die Beschleunigungen durchführt. Dadurch ist er stets weniger gealtert als sein zuhause gebliebener Zwilling.
Zahlenbeispiel zum Zwillingsparadoxon
Letzte Änderung: 15.11.2009
© Joachim Schulz