
Eine Alternative Möglichkeit, das Zwillingsparadoxon zu berechnen, kommt ganz ohne Transformation von Koorinaten aus. Wir brauchen nur ein paar grundlegende Annahmen über Lichtausbreitung und über den Gang von Uhren.
Die Stärke dieses Verfahrens liegt darin, dass nur lokale Messungen der beiden Zwillinge eine Rolle spielen. Es muss keien Annahme über Gleichzeitigkeiten gemacht werden.
Dieses Beispiel ist etwas einfacher gestaltet, als das auf der Seite zum Zwillingsparadoxon: Zwilling Anette (A) steigt in eine Rakete, fliegt 2 Lichtjahre weit mit 80% Lichtgeschwindigkeit zu einem fremden Planeten und kommt mit gleicher Geschwindigkeit zurück. Ihr Bruder Bernd (B) bleibt die ganze Zeit unbeschleunigt auf der Erde.
Das folgende Bild veranschaulicht die Situation:

Nach oben ist wieder die Zeit, nach rechts die Entfernung aufgetragen. Die blaue Linie zweit die Bahn von B. Jedes halbe Jahr ist mit einem Kreis gekennzeichnet. Die rote Linie ist die Bahn von A, die in 2,5 Jahren eine Entfernung von 2 Lichtjahren zurücklegt und dann in gleicher Zeit zurückkehrt. Die schwarzen Linien sind exemplarische Lichtlinien zwischen B und A.
Unabhängig von klassischer oder relativistischer Betrachtung gibt es ein paar Grundannahmen, die in beiden Fällen gleich sind:
Es soll eine Lichtgeschwindigkeit geben, die zumindest in Bs Ruhesystem konstant und unabhängig von der Richtung ist. Wie das aus As Perspektive erscheint, lassen wir erstmal außer Acht.
A fliegt mit 80% Lichtgeschwindigkeit 2 Lichtjahre weit, kommt also nach 2½ Jahren am Planeten an. Licht braucht für dieselbe Entfernung genau 2 Jahre. Insgesamt braucht As Reise aus Bs Perspektive betrachtet 5 Jahre für Hin- und Rückreise. B misst also 5 Jahre für den gesamten Vorgang.
Nun nehmen wir an, A und B haben jeweils baugleiche Taktgeber, die 1000 Takte pro Jahr erzeugen. Jeder Zwilling registriert seine oder ihre eigenen Takte und schickt sie per Laserkommunikation zum anderen Zwilling. Alle erzeugten Takte kommen beim anderen Zwilling an und werden dort registriert.
Bei As Ankunft am Planeten kommt gleichzeitig der 500ste Takt ihres Bruders an, denn der Takt, den B nach einem halben Jahr abgeschickt hat, ist 2 Jahre unterwegs gewesen und kommt daher nach 2½ Jahren bei A an. Dieser 500ste Takt ist im Bild durch die erste schwarze Linie verdeutlicht, die von Bs Halbjahrs-Punkt zu As Ankunft geht. In einem halben Jahr erzeugt B 500 Takte. A hat also während des Fluges 500 Takte von B gemessen. Die Takte ihrer eigenen Uhr nehmen wir zunächst als unbekannte T an. A teilt jetzt die erhaltenen Takte durch die selbst gezählten Takte und erhält die von ihr gemessene Rotverschiebung:
rBA=500/T
A hat während ihres Hinflugs T Signale an B geschickt. Die erreichen B aber erst 2 Jahre nach As Ankunft, also nach 4½ Jahren. Die Signallinie des letzten Hinflug-Signals von A ist im Bild eingezeichnet. In dieser Zeit hat B 4500 Takte gemessen und errechnet daher seine Rotverschiebung zu:
rAB=T/4500
Ähnliche Formeln können für die Blauverschiebung gewonnen werden. In dem Moment, in dem A wieder vom Planeten aufbricht, erhält sie von B das Signal, das er 2 Jahre vorher ausgesandt hat. Also das Signal von 4½ Jahren vor der Rückkehr. Zur Zeit ihrer Ankunft erhält sie Bs letztes Signal. Während der Rückfahrt erhält A also 4500 Signale. Da Rückfahrt und Hinfahrt genau gleich schnell waren, hat A während ihrer Rückfahrt genau dieselbe Anzahl von eignen Signalen T wie während der Hinfahrt gemessen. Ihre Blauverschiebung errechnet sie deshalb zu:
bBA=4500/T
B erfährt von As Rückkehr erst zwei Jahre verzögert, also ein halbes Jahr vor ihrer Ankunft. Er erhält As T Takte also innerhalb eines halben Jahrs, in dem sein Taktgeber 500 zählt. Seine Blauverschiebung ist:
bAB=T/500
In der vor-relativistischen Physik ging man davon aus, dass die Zeit unabhängig vom Bewegungszustand für alle Objekte gleich vergeht. Wenn As Uhr klassisch richtig kalibriert ist, muss sie also für Hin- und Rückflug dasselbe messen, wie A: Die Zeit muss 2½ Jahre sein, A misst T=2500 Takte für Hin- und Rückflug. In die Formeln eingesetzt ergibt das:
rBA=500/T=500/2500=0.2
rAB=T/4500=2500/4500=0.56
bBA=4500/T=4500/2500=1.8
bAB=T/500=2500/500=5
Wir sehen: Der Dopplereffekt ist nicht symmetrisch. B misst mit 0,56 eine schwächere Rotverschiebung als A mit 0,2. B misst mit 5 eine stärkere Blauverschiebung als A mit 1,8. Insbesondere lässt sich anhand des Dopplereffekts messen, wer von den beiden bewegt ist. Das widerspricht dem Relativitätsprinzip.
Das folgende Bild zeigt die Situation in klassischer Interpretation vollständig:

Die schwarzen Linien verdeutlichen den Lauf jedes 500. Signals. A erhält von B 500 Signale während des Hinflugs und 4500 während des Rückflugs. B erhält die 2500 Signale von As Hinflug während der ersten 4½ Jahre und die 2500 Signale von As Rückflug sehr komprimiert im verbeibenden halben Jahr.
Da das hier klassisch gerechnet ist, gibt es kein Zwillingsparadoxon. A ist nach der Rückkehr um dieselben 5 Jahre gealtert wie B.
Die wesentliche Annahme der relativistischen Physik ist, dass alle physikalischen Prozesse unabhängig vom Bewegungszustand des Gesamtsystems sind. Nur relative Geschwindigkeiten dürfen messbar sein. Deshalb können auch die Rotverschiebung und die Blauverschiebung nicht für A und B verschieden sein. Es gibt ja nur eine Relativgeschwindigkeit zwischen ihnen. Es muss also gelten:
rBA=rAB
bBA=bAB
Es folgt aus den Rotverschiebungen:
500/T=T/4500⇒
T2=500·4500=2250000⇒
T=1500
A hat also nur 1500 Takte gezählt. Für sie sind nur 1½ Jahre vergangen. Das ist die Zeitdilatation. Sie kommt hier aus den Grundannahmen durch Rechnen heraus und muss nicht explizit postuliert werden.
Setzen wir nun die Berechneten 1500 Takte in die Gleichungen ein, so erhalten wir die Rotverschiebung:
rBA=500/1500=rAB=1500/4500=1/3
und für die Blauverschiebung:
bBA=4500/1500=bAB=1500/500=3
Wie Sie durch Einsetzen selbst errechnen können, entspricht das der Formel, die ich auf meiner Seite zum relativistischen Dopplereffekt angegeben habe.
Das folgende Bild verdeutlicht die Situation in relativistischer Interpretation:
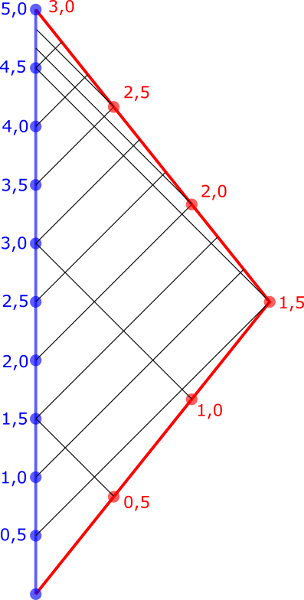
Die Zeitdilatation führt hier dazu, dass für Zwilling A nach der Reise nur 3 Jahre vergangen sind, während für B 5 Jahre vergingen. Wie auch im klassischen Fall, erhält A auf der Hinreise 500 Signale von B und die restlichen 4500 auf dem Rückweg. Allerdings erzeugt Sie jeweils nur 1500 eigene Signale. B erhält die 1500 Hinreise-Signale in sen ersten 4½ Jahren und die 1500 Rückreise-Signal im letzten halben Jahr.
In meinen Augen ist das der eleganteste Weg, das Zwillingsparadoxon zu beschreiben. Er kommt ohne Koordinatenwechsel aus und nur lokale Messungen werden angenommen. Zudem kommen zugleich die richtige Zeitdilatation und der relativistischen Dopplereffekt heraus.
Letzte Änderung: 25.10.2018
© Joachim Schulz