Auf dieser Seite berechne ich den ersten Fall der Lochkamera nach der Relativitätstheorie. Eine Übersicht über die Fälle gibt es in der Einleitung zum Gedankenexperiment Lochkamera.
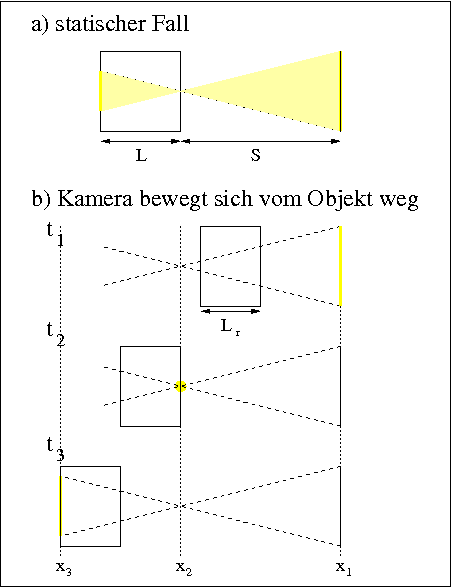
Das folgende Bild zeigt eine statische und eine schnell bewegte Lochkamera. Für die bewegte Lochkamera müssen wir natürlich in Betracht ziehen, dass das Licht nicht überall zugleich sein kann. Ich habe daher drei Zeitpunkte dargestellt: Zur Zeit t1 verlässt das Licht den Schirm, zur Zeit t2 durchquert es die Lochblende und zur Zeit t3 trifft es auf den Film und erzeugt das Bild. Die Position des Lichtblitzes ist in jeder Skizze gelb markiert.
Außerdem muss man sich klar machen, zu welchem Zeitpunkt der Auslöser der Kamera betätigt werden soll. In diesem ersten Fall wird der Kameraverschluss genau zu dem Zeitpunkt geöffnet, and dem sich der Schirm im Abstand S befindet. Dieser Zeitpunkt ist t2.

Im statischen Bild oben sind die Längen gekennzeichnet. Der Abstand vom Objekt zur Lochblende betrage S, die Länge der Kamera sei L. L und S sind Strecken und definieren nach klassischen Strahlensätzen die Verkleinerung des Objektes. Die Verkleinerung beträgt V=L/S.
Im bewegten Fall muss man neben der endlichen Laufzeit des Lichts mit Geschwindigkeit c berücksichtigen, dass nach der Relativitätstheorie die Länge eines bewegten Objektes um den relativistischen Faktor Gamma verkürzt erscheint:
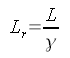
Zahlenwerte für den relativistischen Faktor gibt es auf meiner Umrechnungsseite von Geschwindigkeiten. Den mathematischen Nullpunkt von Ort und Zeit legen wir so fast, dass das Licht zum Zeitpunkt "null Sekunden" am Ortsnullpunkt die Lochblende der Kamera durchqueren soll. Das bedeutet, dass der Verschluss der Kamera zum Zeitpunkt t2 für kurze Zeit geöffnet werden soll.
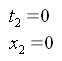
Dabei bezeichnen die Werte x1, x2 und x3 jeweils die Position des Lichtimpulses im relativ zum Objekt unbewegten Koordinatensystem zu den Zeiten t1, t2 und t3. Negative x-Werte bedeuten, dass sich das Licht im Bild rechts vom Nullpunkt befindet. Da sich das Objekt selbst nicht bewegt und das Licht mit Lichtgeschwindigkeit c unterwegt ist, können wir ohne relativistisch rechnen zu müssen angeben:

Vom Zeitpunkt t2=0 ausgehend bewegt sich das Licht mit der Geschwindigkeit c und erreicht zum Zeitpunkt t3 die Raum-Koorinate x3:

Der Film auf der Rückseite der Kamera muss die gleiche Koordinate x3 in der gleichen Zeit t3 erreichen, hat aber einen Vorsprung von der Länge der Kamera, er legt also die geringere Entfernung x3-Lk mit geringerer Geschwindigkeit v zurück:
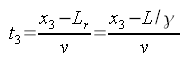
Diese Gleichungen kann man nun nach x3 auflösen

und durch einsetzen von x3 in eine der Formeln für t3 erhält man:

Zuletzt können wir noch die Verkleinerung V als Verhältnis von Bildlänge x3 zu Objektlänge -x1 ausrechnen:

Hierbei habe ich die Definition von Gamma

benutzt.
Die Verkleinerung unterscheidet sich also im Fall der bewegten Kamera vom statischen Fall um einen Faktor, der nur von der Relativgeschwindigkeit v und der konstanten Lichtgeschwindigkeit c abhängt. Im oben definierten Fall, in dem sich die Kamera vom Objekt wegbewegt, ist die Geschwindigkeit positiv und das Bild erscheint auf dem Film grösser. Die gleichen Formeln kann man jedoch auch anwenden, wenn sich die Kamera auf das Objekt zu bewegt. In dem Fall wir das Bild kleiner. (Hier die Zeichnung dazu.) Wenn aber das Relativitätsprinzip stimmen soll, muss die Verkleinerung gleich sein, wenn sich nicht die Kamera sondern das Objekt bewegt, die Natur kennt ja nur Relativbewegungen und keine absolute Bewegung. Der Fall des bewegten Objekts lässt sich mit Hilfe der Lorentztransformation leicht lösen:
Zur Erinnerung ist hier nochmal die Skizze der statischen Lochkamera:

Hier gerät man leicht in die Versuchung einfach anzunehmen, dass nun der Objektabstand S um den gleichen Faktor verkürzt ist wie vorher der Kameraabstand:

Damit würde das Bild um den Kehrwert von Gamma größer und nicht um den oben angegebenen Wert. Dies wäre ein Widerspruch, denn auf dem Film kann sich ja nur ein Bild befinden, unabhängig davon, aus welchem Bilckwinkel man die Entstehung betrachtet.
Dieser scheinbare Widerspruch löst sich auf, wenn man bedenkt, dass die einfache Längenkontraktion nach der Formel S2=S/Gamma nur für einen Moment, nämlich zur Zeit t2=0 gelten kann. Schließlich bewegt sich das Objekt relativ zur Kamera und sein Abstand zur Kamera muss sich ständig ändern. Wir müssen also die vollständige Lorentztransformation nach den Formeln
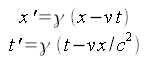
verwenden. Hier bedeuten die Größen mit Strich, die Orts- und Zeitkoordinaten im System, in dem die Kamera ruht und das Objekt sich mit v bewegt. Danach ergibt sich folgendes Bild:

Man sieht auf dem ersten Blick, dass sich eine Vergrößerung des Bildes relativ zum Bild der statischen Kamera ergibt, die dem oberen Bild der bewegten Kamera entspricht. Diesmal aber nicht Aufgrund der Bewegung der Kamera, sondern aufgrund von Bewegung des Objektes und relativistischer Verkürzung des Objektabstandes.
Wir wollen jetzt mit der Lorentztransformation berechnen, ob tatsächlich die gleiche Vergrößerung herauskommt: Die Lorentztransformation ändert grundsätzlich nicht den Nullpunkt des Koordinatensystems. Es gilt also auch im Ruhesystem der Kamera:
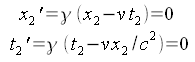
Nun können wir überprüfen, ob die Kamera nach der Lorentztransformation tatsächlich die Länge einer ruhenden Kamera hat:

Um die Verkleinerung V' zu bekommen brauchen wir nun noch die Position des Objekts zur Zeit der Lichtabstrahlung:

Schließlich können wir die Verkleinerung V' im Ruhesystem der Kamera berechnen:

Erwartungsgemäß ergibt sich das gleiche Bild auf dem Film, wenn man die Aufnahme aus der Sicht der ruhenden Kamera betrachtet, wie wenn man die Aufnahme aus der Sicht des ruhenden Objektes sieht. Die Rechnung zeigt also, dass die Lorentztransformation dem Relativitätsprinzip genügt.
Eine weitere Forderung der Relativitätstheorie ist, dass die Lichtgeschwindigkeit in jedem Bezugssystem den gleichen Wert c hat. Ob diese Forderung in dem Gedankenexperiment erfüllt ist lässt sich leicht Prüfen. Die Lichtgeschwindigkeit errechnet man, indem man die vom Licht zurückgelegte Strecke durch die dazu gebrauchte Zeit teilt. Wir haben hier zwei Strecken: x1 nach x2 ist die Strecke vom Objekte zur Lochblende und x2 nach x3 ist die Strecke von der Lochblende zum Film. Da x2 als Nullpunkt der Ortsskala definiert ist und das Licht dort zur Zeit t2=0 Sekunden ankommt. Lässt sich die Lichtgeschwindigkeit leicht berechnen zu x1/t1 und x3/t3. Für die ungestrichenen Größen habe ich die Zeiten und Orte oben bereits ausgerechnet. Für die gestrichenen Größen, also die im Ruhesystem der Kamera kennen wir schon die Orte x'1 und x'3. Die dazugehörigen Zeiten berechnet man über die Lorentztransformation zu

und

Wenn wir jetzt alle berechneten Orte und Zeiten einsetzen, können wir leicht überprüfen:
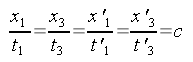
Die Lichtgeschwindigkeit ist also wie erwartet in beiden Bezugssystemen für jeweils beide Strecken gleich c. Damit ist das Relativitätsprinzip erfüllt.
Letzte Änderung: 12.12.2005
© Joachim Schulz