
Auf diesen Seiten möchte ich darstellen, wie man das Beispiel einer relativistisch schnell bewegten Lochkamera unter Berücksichtigung der Relativitätstheorie rechnet. Dazu zunächt mal ein paar Worte zu einer statischen Lochkamera: Eine Lochkamera ist einfach ein Kasten mit einem kleinen Loch ohne Linse. Die Abbildung des Objektes auf dem Film erfolgt also nur über Strahlengesetze und nicht über die Brechung von Licht über Linsen. Dadurch handelt es sich um ein einfaches Beispiel, bei dem zum Beispiel der relativistische Dopplereffekt keinen großen Einfluss hat.
Bei einer relativen Bewegung zwischen Kamera und Objekt ist es natürlich nicht unerheblich zu welchem Zeitpunkt der Verschluss der Kamera geöffnet wird um die Aufnahme zu machen. Ich möchte auf diesen Seiten zwei Fälle betrachten. Auf dieser Seite sind die Bewegungen für beide Fälle aus der Sicht der Kamera beschrieben. Die Beschreibungen aus der Sicht des Objektes folgen auf den einzelnen Seiten zu den Fällen.
Auf der folgenden Grafik ist der erste Fall dargestellt:

Dieser erste Fall beschreibt die Aufnahme eines bewegten Objekts unter der Voraussetzung, dass der Kameraverschluss genau in dem Moment betätigt wird, in dem das Objekt eine bestimmte Entfernung von der Kamera hat. Diese Entfernung ist zum Zeitpunkt des Lichtdurchtritts (zweiter Zeitschritt) mit Sr bezeichnet. Das sich der Kamera nähernde Objekt erscheint auf dem Film weiter entfernt, weil das Licht bereits vorher (im ersten Zeitschritt) das Objekt verlassen hat. Zu dieser Zeit war das Objekt noch weiter von der Kamera entfernt. Hier geht es zur relativistischen Berechnung der Lochkamera für den ersten Fall.

Der zweite Fall sieht viel einfacher aus, ist in der Praxis aber komplizierter, weil die Lichtlaufzeit beachtet werden muss. Das Licht verlässt hier in dem Moment das Objekt, in dem es den Abstand S von der Kamera hat. Der Verschluss der Kamera wird so betätigt, dass dieses Licht gerade hineinfällt. In welche Richtung sich das Objekt bewegt ist hier unerheblich, da bei der Belichtung die Lichtlaufzeit berücksichtigt wird. Hier geht es zur Berechnung der relativistischen Lochkamera für den zweiten Fall.
Beide Beispiele habe ich in der Näherung kleiner Einfallwinkel gerechnet. Das bedeutet, dass die Ergebnisse nur unter der Bedingung exakt sind, dass die Entfernung des Objektes von der Kamera wesentlich grösser ist als die Objektgröße. Was sich ändert, wenn man diese Näherung aufgibt, kann man anhand folgender Grafik erläutern:
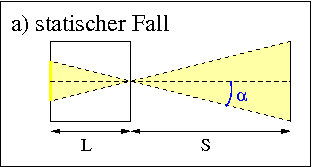
Hier habe ich in die Grafik der ruhenden Kamera den Einfallswinkel α eingezeichnet. Das Licht, das vom Rand des Objektes ausgeht durchläuft also nicht die Strecke S zur Kamera und L innerhalb der Kamera, sondern die längeren Strecken S/cos(α) und L/cos(α). Da das Licht stets mit Lichtgeschwindigkeit unterwegs ist, verlängern sich somit die Zeiten in den Rechnenbeispielen um gleiche Faktoren, die sich dann nach dem gleichen Muster in der Lorentztransformation transformieren. Qualitativ kommt jedoch für die Objektgröße das selbe heraus. Für kleine Winkel α ist der Kosinus nahe eins, so dass man in guter Näherung so rechnen kann, wie ich es hier dargestellt habe.
Bei großen Winkeln muss man eine zusätzliche Verzerrung des Objektes aufgrund der Bewegung berücksichtigen. Die Strahlen, die gleichzeitig das Objekt verlassen, erreichen die Öffnung der Lochkamera nicht gleichzeitig. Solche Verzerrungen werden auf der Seite Tempolimit Lichtgeschwindigkeit dargestellt.
Um rechnerisch auf die richtigen Ergebnisse zu kommen, muss man festlegen, in welche Richtungen die Orts- und Geschwindigkeitsskala verlaufen soll. Hier bin ich in beiden Fällen so vorgegangen, dass die Ortskoordinate von rechts nach links zunimmt und die Relativgeschwindigkeit positiv ist, wenn sich Kamera und Objekt voneinander entfernen. Die gewöhnliche Lorentztransformation muss für die Transformation vom Ruhesystem des Objekts zum Ruhesystem der Kamera verwandt werden, da die Kamera in allen Grafiken links vom Schirm ist und damit bei positiver Relativgeschwindigkeiten in positiver Richtung fliegt. Für die Transformation vom Ruhesystem der Kamera ins Ruhesystem des Objekts wird sie Rücktransformation verwandt.
Letzte Änderung: 16.12.2005
© Joachim Schulz