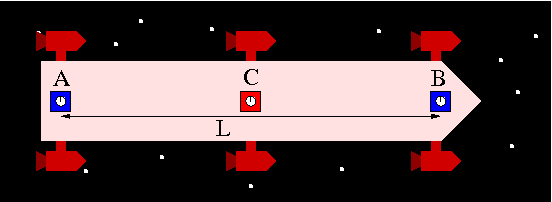
Auf dieser Seite möchte ich berechnen, wie sich eine relativistische Beschleunigung auf Abstände und Gleichzeitigkeit in einer Rakete auswirkt. Dieses Gedankenexperiment zur relativistischen Beschleunigung habe ich auf der vorherigen Seite beschrieben. Hier ist nochmal das Bild zur Erinnerung:

Das nächste Bild stellt den zeitlichen Ablauf schematisch dar:

Nach oben ist die Zeit aufgetragen, nach rechts die Position. Ein unbewegtes Objekt wird also durch eine senkrechte Linie dargestellt. Unterhalb der x-Achse stellen drei blaue senkrechte Linien die Positionen der Geräte A, B und C dar (C ist in der Mitte). Die x-Achse kennzeichnet den Zeitpunkt der Beschleunigung. Dieser Zeitpunkt soll den Zeitnullpunkt (t=0) darstellen. Das Gerät A befindet sich vor der Beschleunigung am Ortsnullpunkt (x=0) und das Gerät B befindet sich im Abstand L an der Spitze der Rakete (x=L).
In der Relativitätstheorie spielen Ereignisse eine große Rolle. In unserem Beispiel gibt es vier Ereignisse, die mit kleinen Buchstaben bezeichnet sind. Als Ereignisse a und b bezeichne ich das Aussenden der Lichtblitze von den Geräten A und B. Aus der Sicht der unbewegten Rakete geschieht das gleichzeitig im Moment der Beschleunigung. Die Raum- und Zeitkoordinaten dieser Ereignisse lauten einfach:

Etwas komplizierter ist es sich klar zu machen, wann und wo die Ereignisse c und d stattfinden. Hiermit bezeichne ich das Auftreffen der Lichtblitze an der Kontrollbox C. Die Zeit, zu der der Lichtblitz von Gerät B eintrifft, ist gegeben durch die Entfernung von B zu C (L/2) und die Geschwindigkeit mit der die Kontrollbox und der Lichtblitz aufeinander zueilen. Der Lichtblitz bewegt sich dabei mit Lichtgeschwindigkeit c und die Kontrollbox mit der Raketengeschwindigkeit v. Da die Bewegungen aufeinander zu laufen, müssen die Geschwindigkeiten addiert werden. Der Ort ergibt sich aus der Anfangsposition der Kontrollbox (x=L/2) und dem seit dem zurückgelegten Weg. Damit ergeben sich Zeit und Ort von Ereignis c zu:

Für Ereignis d errechnet man Zeit und Ort auf die gleiche Weise, nur dass sich die Kontrollbox von dem Lichtblitz wegbewegt und man daher die Differenz der Geschwindigkeiten nehmen muss:

Die bisher angegebenen Orte und Zeiten sind alle aus der Sicht eines nicht mitbeschleunigten Beobachters angegeben. Wenn wir es mit kleinen Geschwindigkeiten zu tun haben und daher klassische Physik angewandt werden kann, hat sich nach der Beschleunigung nichts geändert. Alle Geräte sind an ihrem Ort geblieben und die Uhren sind nach wie vor synchronisiert. Für Geschwindigkeiten, die mit Lichtgeschwindigkeit vergleichbar sind, macht die spezielle Relativitätstheorie jedoch andere Voraussagen. Sowohl Orte als auch Zeiten ändern sich:
Um zu berechnen, wie die Ereignisse aus Sicht der Raketenbesatzung nach der Beschleunigung aussehen, wird die Lorentztransformation verwendet:
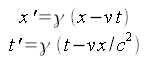
wobei der Gamma-Faktor von der Geschwindigkeit abhängt:

Ich führe die Transformation am Ereignis a aus, so dass sich für dieses Ereignis nichts ändert:

Die Wahl des Transformationspunktes ist willkürlich, hat aber keinen Einfluss auf die berechneten Abstände und Dauern.
Das erste interessante Ergebnis ergibt sich, wenn man den Ort der Raketenspitze (Gerät B) berechnet. Hier ergibt sich durch einsetzen in die Transformationsgleichungen:
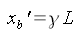
Da der relativistische Faktor Gamma immer größer als eins ist, bedeutet dieses Ergebnis, dass die Rakete nach der Beschleunigung um den Faktor Gamma auseinandergezogen ist. Wenn man annimmt, dass das Material, aus dem die Rakete besteht, elastisch ist, wird sich die Rakete während des Fluges wieder auf ihre ursprüngliche Länge zusammenziehen. Da dieser Vorgang jedoch Materialabhängig ist und nichts mit der Relativitätstheorie zu tun hat werde ich das hier nicht weiter behandeln.
Mit der Lorentztransformation kann man auch den Zeitpunkt der Beschleunigung aus der Sicht der bewegten Rakete berechnen:
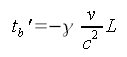
Es ergibt sich eine negative Zeit. Die Uhr im Gerät B, die zum Zeitpunkt der Beschleunigung Null anzeigt, geht also durch die Beschleunigung um den einen vom Abstand L und der Geschwindigkeit abhängigen Betrag vor. Dass die Uhren nach der Beschleunigung nicht mehr synchron gehen, kann die Besatzung jedoch nicht direkt ablesen, hierzu sind die Ereignisse c und d an der Kontrollbox C vorgesehen. Die Berechnung der Orte dieser Ereignisse ergibt keine Überraschung:

Alle Entfernungen sind um den gleichen Faktor Gamma vergrößert.
Der Sinn der Kontrollbox in der Mitte zwischen Bug- und Heckuhr ist jedoch, dass dort die Zeitdifferenz der beiden Uhren direkt abgelesen werden kann. Kommen die Signale beider Uhren gleichzeitig an, so sind die Uhren synchronisiert. Eine Zeitdifferenz zwischen den beiden Signaleingängen gibt dagegen an, wie weit die Uhren auseinandergelaufen sind.
Das Signal der Buguhr erreicht die Kontrollbox zur Zeit:

Hier gibt der erste Summand an, um wieviel die Uhr der Kontrollbox aus der Sicht von A vorgeht. Das ist genau die Hälfte der Zeit tb', da C halb so weit von A entfernt ist. Auf gleiche Weise lässt sich die Zeit berechnen, an der das Signal der Heckuhr A ankommt bei der Kontrollbox ankommt:
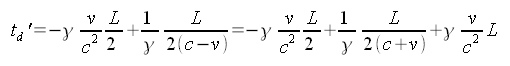
Auch hier gibt der erste Summand die Zeitverschiebung an der Box C an. Die Kontrolbox kann nun aus der Zeitdifferenz ermitteln, wie stark die Uhren A und B voneinander abweichen:

Es kommt genau der Wert heraus, den man aus der Errechnung von tb' erwartet. Die Relativität der Gleichzeitigkeit ist also in diesem Beispiel messbar.
In dieser Beispielrechnung wurde der Einfachheit halber auf die Berechnung der Kontraktion der Rakete bei der Beschleunigung verzichtet. Tatsächlich werden die Bindungskräfte der Materialien währen einer nicht zu starken Beschleunigung dafür sorgen, dass sich die Rakete entsprechend der Längenkontraktion um den Faktor Gamma verkürzt. Bei der verkürzten Rakete ist statt der Länge L also die Länge

einzusetzen. Damit ergibt sich dann für den Zeitunterschied zwischen Bug und Heck der Rakete die Formel:
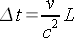
Diese Formel ist nicht nur für beschleunigte Systeme sinnvoll, sondern kann wegen der Ähnlichkeit von Gravitation und Beschleunigung auch zur Berechnung der gravitativen Zeitdilatation verwendet werden.
Letzte Änderung: 31.08.2007
© Joachim Schulz