Im Abschnitt zu den erdgebundenen Koordinaten habe ich erläutert, dass die spezielle Relativitätstheorie nicht nur in Inertialsystemen funktioniert. Auch nicht inertiale Systeme können mit der speziellen Relativitätstheorie berechnet werden. Sie zeichnen sich dann durch Scheinkräfte aus und dadurch, dass die Lichtgeschwindigkeit nicht unbedingt überall gleich ist.
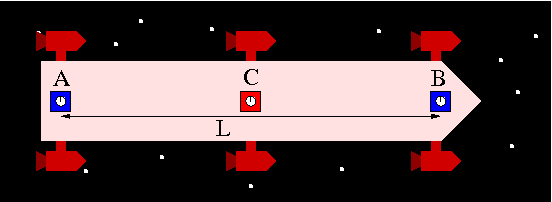
Hier möchte ich nun Effekte von gleichmäßig in einer Richtung beschleunigten Koordinaten beschreiben. Man kann sich dazu eine Rakete vorstellen, wie ich sie in meinem Gedankenexperiment zur Beschleunigung gezeichnet habe:
Beschleunigt eine Rakete im freien Raum gleichmässig, so nimmt ihre Geschwindigkeit ständig zu. Die Astronauten an Bord werden von den Sitzen, in denen sie sich befinden, ständig nach vorne beschleunigt und spüren so einen Druck von den Stühlen. Allgemein geht von den Triebwerken eine Spannung aus. Die Triebwerke ziehen die Rakete mit sich. Lassen die Astronauten einen Gegenstand los, so bewegt dieser sich nur gleichmäßig mit der Geschwindigkeit, die er zum Zeitpunkt des Loslassens hatte. Er bleibt also immer weiter hinter der beschleunigenden Rakete zurück.
Aus der Sicht eines Astronauten ist es natürlicher, die Koordinaten relativ zur Rakete zu definieren. Also so, dass man zum Beispiel die eingezeichnete Uhr A immer an den selben Koordinaten wiederfindet. In solch einem mitbewegten Koordinatensystem wird man die gleiche Spannung feststellen, die von den Triebwerken ausgeht. Die Raumfahrer sehen aber nichts von einer Beschleunigung durch die Sitze, sie spüren nur eine Kraft, die sie gleichmäßig in ihre Sitze presst. Wenn sie einen Gegenstand loslassen, dann beobachten sie, wie er mit einer konstanten Geschwindigkeitsänderung nach hinten beschleunigt. Alle diese Beobachtungen kann man beschreiben, indem man dem gesamten Raum in der Rakete eine Fallbeschleunigung zuordnet. Jeder losgelassene Körper fällt mit gleicher Beschleunigung gegen die Rakete zurück.
Bereits hier wird eine starke Ähnlichkeit eines beschleunigten Koordinatensystems mit dem Schwerefeld der Erde deutlich. Lassen wir einen Gegenstand auf der Erde los, so fällt er unabhängig von seiner Masse mit konstanter Beschleunigung. Er wird in jeder Sekunde 9,81 Meter pro Sekunde schneller. Auf der Erde wird das mit einer Anziehungskraft zwischen Massen, der Gravitation, erklärt und nicht damit, dass die Erde beschleunigt ist. Auch im beschleunigten Koordinatensystem könnte man nun auf die Idee kommen, die Beschleunigung auf eine massenabhängige Kraft zurückzuführen, die Trägheitskraft. Und genau diese Kraft ist es, mit denen sich die Raumfahrer in die Stühle gepresst fühlen. Der Andruck ist von dem Gewicht des Raumfahrers abhängig. Die Ähnlichkeit zwischen beschleunigten Koordinatensystemen und Gravitation geht also ziemlich weit. Bevor ich darauf zurückkomme, möchte ich aber noch auf die Effekte der speziellen Relativitätstheorie in einem beschleunigten System eingehen.
relativistische Effekte
Aus der Relativität der Bewegung und der Invarianz der Lichtgeschwindigkeit folgt, dass Gleichzeitigkeit relativ ist. Das wird beim Zwillingsparadoxon deutlich: In der Beschleunigungsphase des reisenden Zwillings scheint ihm die Zeit des zurück gebliebenen Zwillings, in dessen Richtung er beschleunigt, schneller zu gehen. Die Zeit der Objekte, von denen er weg beschleunigt, vergeht langsamer. Dieser Effekt tritt auch in der beschleunigenden Rakete auf. Im Gedankenexperiment zur Beschleunigung habe ich das berechnet. In der oben gezeichneten Rakete ergibt sich, dass die Zeit um so schneller läuft, je weiter vorne sie gemessen wird. Uhr B geht schneller als Uhr C und diese geht wieder schneller als Uhr A. Dieser Effekt ergibt sich aus den geometrischen Betrachtungen der Relativität der Gleichzeitigkeit. Obwohl die Uhren exakt der gleichen Beschleunigung unterliegen, gehen sie unterschiedlich schnell. Ursache ist ihre unterschiedliche Lage im beschleunigten Koordinatensystem. In einem beschleunigten Koordinatensystem vergeht die Zeit nicht mehr an jedem Ort gleich schnell.
Ein weiterer Effekt ergibt sich aus der Längenkontraktion. Die beschleunigte Rakete ändert von außen betrachtet ständig die Geschwindigkeit und müsste darum immer kürzer werden. Wenn aber (wie hier gezeichnet) drei Triebwerke gleichmäßig ziehen, muss eine zusätzliche Materialverspannung auftreten. Damit die Rakete ihre Länge beibehält, dürfen die Beschleunigungen also gar nicht gleich stark sein. Die Rakete kann nur verzerrungsfrei beschleunigt werden, wenn das vordere Triebwerk eine geringere Leistung bringt als das hintere. Dieser Effekt passt gut zum unterschiedlichen Uhrengang: Da vorne die Zeit schneller läuft, muss das vordere Triebwerk weniger Energie pro Zeiteinheit (das ist Leistung) liefern um eine verzerrungsfreie Beschleunigung zu gewährleisten.
In dem hier genannten Beispiel mit drei gleichmäßig beschleunigten Triebwerken, wird die Rakete also für den außenstehenden Beobachter die gleiche Länge behalten, aber aus Sicht der Raumfahrer mehr und mehr in die Länge gezogen werden. Werden die Triebwerke dagegen so gesteuert, dass sie keine Spannung erzeugen, (dazu muss das vordere Triebwerk gedrosselt werden,) so wird sich die Rakete für einen außenstehenden Beobachter nach der bekannten Längenkontraktion zusammenziehen.
Ereignishorizont
Ein erstaunlicher Effekt in einem beschleunigten Koordinatensystem ist die Existenz eines so genannten Ereignishorizontes. Ein Ereignishorizont ist eine Fläche, die Lichtsignale nur in eine Richtung durchqueren können. Signale können in den Ereignishorizont hineingesandt werden, sie können aber nicht hinauskommen.
Betrachtet man die Rakete wieder von außen, so findet sich ein Punkt hinter der Rakete, von dem aus ein Lichtsignal die Rakete nie erreichen wird. Der Lichtstrahl ist zwar immer schneller als die Rakete, aber aufgrund der ständigen Beschleunigung vergeht beliebig viel Zeit in der Rakete, ohne dass der Lichtstrahl die Rakete erreicht.
Wie weit der beschriebene Punkt hinter der Rakete liegt, hängt nur von der Stärke der Beschleunigung ab. Je stärker die Beschleunigung ist, desto dichter liegt der Ereignishorizont, der komplett schwarz erscheint, hinter der Rakete. Der Ereignishorizont entspricht dem Punkt, an dem die Zeitdilatation durch Beschleunigung so stark ist, dass die Zeit stehen bleibt. Hinter dem Ereignishorizont vergeht die Zeit im beschleunigten Koordinatensystem rückwärts. Da aber von dort keine Signale die Rakete erreichen können, hat das keinen Einfluss auf die Kausalität, die eine eindeutige Zeitrichtung erfordert. Ereignisse, die hinter dem Ereignishorizont der Rakete geschehen, können auf die Rakete keinen Einfluss nehmen. Sie können also nicht eindeutig der Vergangenheit der Rakete zugeordnet werden.
Übergang zur allgemeinen Relativitätstheorie
Hat man sich die Effekte der speziellen Relativitätstheorie in beschleunigen Systemen erarbeitet, so ist es relativ leicht die Grundlagen der allgemeinen Relativitätstheorie zu verstehen. Im nächsten Abschnitt werde ich nun auf die Gravitation durch Raum-Zeit-Krümmung, wie sie in der allgemeinen Relativitätstheorie beschrieben wird, eingehen